Monitoring body composition in athletes is beneficial for many reasons. Skinfold thickness assessment is one of many methods that can be used to accomplish this task. How skinfolds assessment works, its popularity among sports professionals, how to pick the right equation to use, and sources of error are reviewed in this article.
Grey boxes are summary points
Blue boxes give more detail about key terms or subjects
How Skinfold Assessment Works
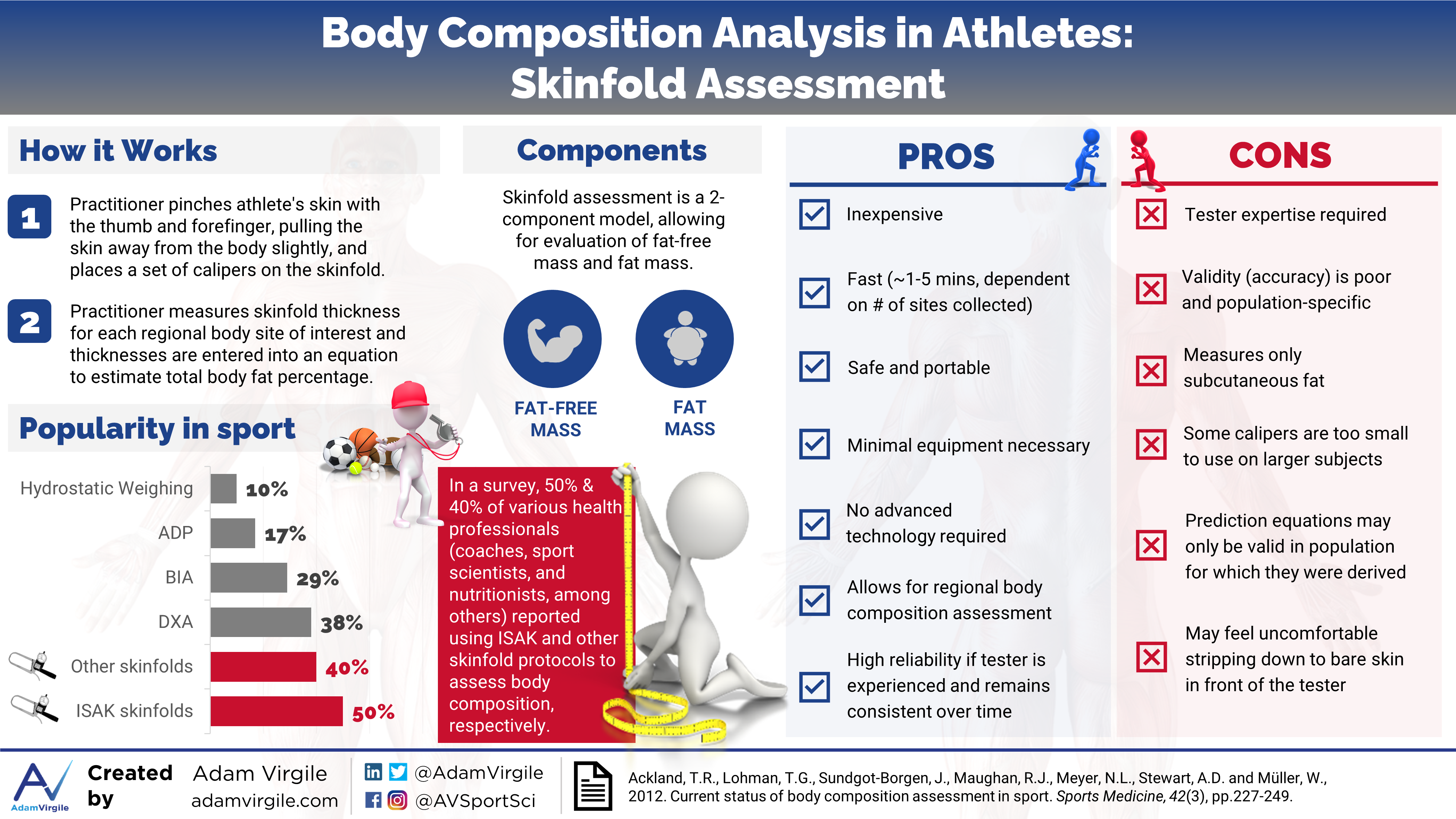
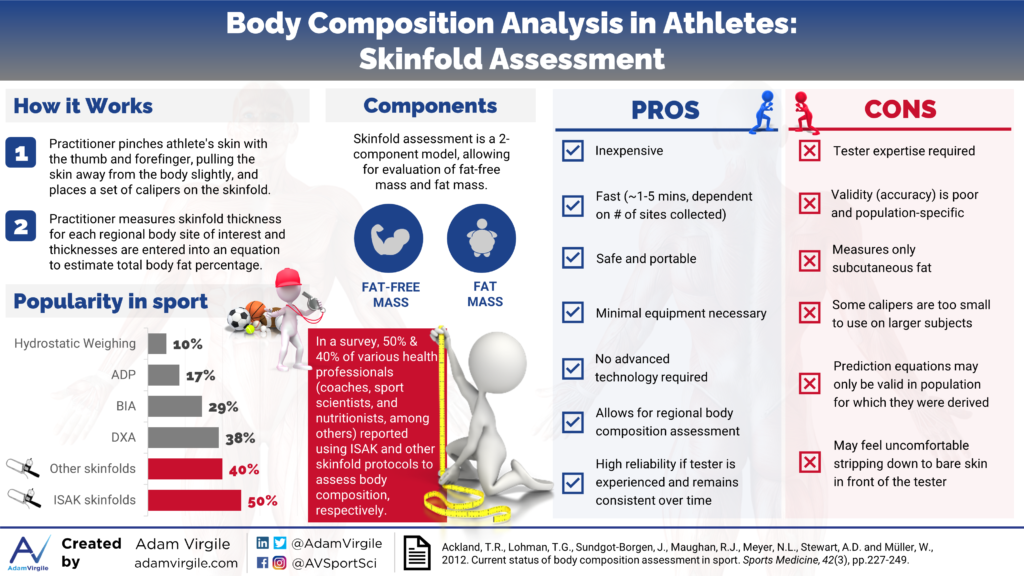
Anthropometry involves the measurement of body dimensions, which can include height, weight, length, width, circumference, and skinfold thickness [1]. For example, examining the difference in circumference of the waist and hip is deemed the waist-to-hip ratio, and is a common anthropometric assessment for general health. Body Mass Index (BMI) is a commonly used index of relative weight to height. In sport, body composition is oftentimes estimated by measuring the thicknesses of various skinfold sites on the body. To take a skinfold measurement, a practitioner pinches the athlete’s skin with the thumb and forefinger, pulling the skin away from the body slightly, and places a set of calipers on the skinfold [2]. This measurement estimates the thickness of the subcutaneous fat tissue that lies underneath the skin.
BMI = Body mass index. An indicator of relative body size using an individual’s body weight and height. Calculated by dividing body weight in kilograms by the square of height in meters (kg/m2). BMI can be used to screen for weight categories that may lead to health problems, but it is not diagnostic of body fatness or health of an individual because it does not consider body fat percentage. The BMI classification categories are outlined below:
Underweight: <18.5
Normal weight: 18.5 to 24.9
Overweight: 25 to 29.9
Obese Class 1 (low-risk): 30 to 34.9
Obese Class 2 (moderate-risk): 35 to 39.9
Obese Class 3 (high-risk): 40+
Popularity
Assessing body composition with skinfold measurements is by far the most prominent technique used by sport professionals [3]. Various skinfold techniques and body composition estimation equations exist (more on this later). In an effort to standardize measurements, guidelines for the anatomical location of skinfold sites and measurement technique have been published [4, 5], most recently by the International Society of Kinanthropometry (ISAK), [6].
ISAK = International Society for the Advancement of Kinanthropometry. A recognized organization that has defined and approved an international anthropometry accreditation scheme which is used throughout the world to train and accredit people in anthropometry.
The ISAK protocol, collecting a maximum of 8 skinfold sites, is the most frequently used among skinfold techniques [3]. In Oceania, ISAK skinfolds are more popular than all other techniques, according to the 28 sport professionals surveyed in 2013; a whopping 82% of professionals in this area used ISAK skinfolds for body composition assessment, whereas only 25% used any other skinfold technique [3]. In the Americas and in Europe, other skinfold techniques are more popular. In the Americas, 24% and 34% of the 92 surveyed sport professionals used ISAK and other skinfold methods, respectively. In Europe, 47% and 51% of the 55 surveyed sport professionals used ISAK and other skinfold methods, respectively. In all locations, a form of skinfold assessment was the most popular method for quantifying body composition [3].
Assumptions and Equation Madness
All assessment methods make assumptions to estimate body composition because it’s impossible to measure composition directly, other than post-mortem dissection and cadaver analysis. Many assumptions tend to be made when using skinfolds to assess body composition. A few of these assumptions include: (1) skinfold thickness is a good measure of subcutaneous fat, (2) there’s a fixed relationship between subcutaneous and internal fat tissue, (3) skinfold compressibility is constant, and (4) there’s consistent fat patterning across the body [7].
Since the relationship between subcutaneous and total body fat can be dependent on various factors such as age, sex, and health status [1, 2], hundreds of prediction equations have been developed, each with its own “secret sauce” for estimating how these factors affect the validity of predictions. Ultimately, once the skinfolds are measured, the sum of skinfold thicknesses, and ratios between measurement sites, are inserted into a calculation to predict the fat mass and fat-free mass of the athlete. As of 2012, more than 100 different body fat prediction equations using various combinations of anthropometric measurements had been reported in the literature [1, 7, 8]. The number of available equations to choose from continues to increase.
Sorting through the sea of equations to choose the one that’s most appropriate is a tall order for any practitioner; the process can be both overwhelming and confusing.
When skinfold assessments are the chosen method of body composition assessment, finding the right equation can become a hazardous endeavor; I’m going to try to help with that but let’s, first, take a brief look at the history, and progression of skinfold equations to get a lay of the land.
Where it All Began
Given skinfold assessment simplicity and lack of required technology, it has been used to predict body density and total body fat for a long time. Using observations made by Edwards (1950) on 53 different skinfold sites [9], Ancel Keys and Josef Brozek published the first valid skinfold equations to estimate body fat percentage in 1951 [10]. Since then, over 100 prediction equations using various combinations of anthropometric variables have been developed and reported in the literature, with more than 19 different sites for measuring skinfold thickness having been described in detail [1, 7, 8].
The Most Popular Equations
In 50 of the most frequently used equations from the literature, the standard error of estimate (SEE) ranges from 3-11%, with most prediction equations having an SEE within 3-7% [8]. The SEE is a measure of the accuracy of predictions when compared with highly accurate methods, such as dual energy x-ray absorptiometry (DXA) and air displacement plethysmography (ADP). The two most popular equations are those developed by Jackson & Pollock, and Durnin & Wormersley [8]. Jackson and Pollock’s equations use combined gender, age, and the sum of 3 or 7 skinfolds [11, 12], and Durnin and Womersley’s equation uses combined age and sum of 4 skinfold sites [13]. The most popular equation is one of the two equations developed by Jackson and Pollock in 1978, using three skinfold sites: the chest, abdomen, and thigh [12]. These classic prediction equations were considered to be valid when compared against underwater weighing (UWW); before ADP, and later, DXA validation, underwater weighing (UWW) was considered the “gold standard” for body composition assessment [14-16].
DXA = Dual energy x-ray absorptiometry. Passes filtered x-ray beams with two different photon energies (emitting a very small dose of ionizing radiation) through the body to produce pictures of the inside of the body and is considered one of the “gold standard” methods for body composition assessment. DXA can estimate the breakdown of (1) lean mass, (2) fat mass, and (3) bone mineral content, by body segment, because each tissue differentiates photons differently.
ADP = Air displacement plethysmography. The subject is required to sit inside an enclosed chamber (plethysmograph), most commonly measured via a device called the BOD POD, and is considered another “gold standard” method for body composition assessment. It estimates the subject’s body volume from the air that gets displaced when the subject is in the chamber, and using Boyle’s law (and the Siri equation), ADP estimates the breakdown of (1) lean mass, and (2) fat mass, inside the body.
UWW = Underwater weighing. The subject is required to exhale all of the air from their lungs (or as much as possible), and then be weighed underwater, which requires full-body submersion. UWW is considered another “gold standard” method for body composition assessment. Conceptually, it’s similar to ADP, but is based on Archimedes’ principle and estimates the subject’s body volume from the volume of water that gets displaced when underwater. UWW estimates the breakdown of (1) lean mass, and (2) fat mass, inside the body.
The New Age of Skinfold Equations and 3 vs. 7 Sites
More recently developed skinfold regression equations are derived from four-compartment methods (underwater weighing, or UWW, is a two-compartment method), which, theoretically, should provide improved accuracy for body composition assessment via skinfold measurements.
Peterson et al. (2003) developed an equation that was reported to be more accurate than the two aforementioned classic equations by Durnin and Womersley, and Jackson and Pollock [17]. Peterson et al. (2003) consider four skinfold sites, height, age, and body weight (body weight in women only) in their prediction equation [17]. Relevant to the athletic cohort, Evans et al. (2005) generated prediction equations using a diverse group of collegiate athletes [18]. This research group produced very accurate 7-site and 3-site prediction equations; gender and race are also considered [18]. Similar to the classic work of Keys and Brozek in 1953 [10] and investigations in highly trained athletes [19-23], Evans’ research group found that there were no differences between using fewer (i.e. 3) vs. more (i.e. 7) skinfold sites for predicting body composition [18].
The total body of research suggests that there is merely a slight difference, if any at all, between the precision of 3-site and 7-site skinfold prediction equations.
An Ultrasound Teaser
Despite the advancements in skinfold testing, new research using ultrasound (US) imaging techniques shows that any caliper-based skinfold assessment method lacks validity relative to its US-based counterpart [23-25]. This is primarily because skinfold-pinching measures a compressed double layer of subcutaneous adipose tissue and skin, whereas the US technique measures only the metric of interest, uncompressed subcutaneous adipose tissue, with high accuracy [24]. The use of ultrasound (US) as a body composition assessment tool is discussed in more detail, here.
US = Ultrasound. Using a beam of skin-penetrating ultrasonic waves (i.e. high-frequency sound waves above the upper limit of human hearing) emitted by a transducer probe, body fat percentage is estimated based on the acoustic impedance of different tissue borders. Similar to skinfold assessment, ultrasound is used to assess regional subcutaneous fat tissue. However, ultrasound measures the subcutaneous fat tissue thickness in a decompressed state (i.e. single layer), whereas skinfold assessment requires pinching of the skin and subsequent measurement of the same tissue in a compressed state (i.e. double layer). Using a prediction equation, US estimates the breakdown of (1) lean mass, and (2) fat mass, inside the body.
Picking the Right Equation
There have been many studies in athletes where comparisons were made between various skinfold equations and “gold standard” criterion reference measures. López-Taylor (2018) recently investigated 31 different anthropometric equations against DXA in 131 male soccer players of varying ethnicities [19]. Of these 31 equations, 14 and 17 were developed in athletic, and nonathletic populations, respectively. In general, the equations developed in athletes that had the highest agreements with DXA, with an equation by Civar et al. [26] having the strongest association with DXA. Ironically, an equation using a mere two skinfold sites (abdomen and thigh) developed in male nonathletes by Wilmore and Behnke [27] was more closely related with DXA, compared with the other equations developed in athletes.
The results of this study differ from those obtained from anthropometric comparisons in other male soccer players. In 45 professional male soccer players from the Premier League [28], a 7-site skinfold equation developed by Withers et al. [29] proved to be the most accurate and highly correlated with DXA-derived body fat percentage, compared with the 8 other skinfold equations investigated, including the aforementioned classic equation developed by Durnin and Womersley [13]. Recently, Suarez-Arrones et al. (2018) investigated how body composition assessments using 8 different skinfold equations and bioelectrical impedance (BIA) fared against DXA, in 18 elite male soccer players [30]. With the exception of one equation created by Deurenberg et al. in 1991 [31], and BIA via a Tanita device, body fat percentages derived from all skinfold equations had moderate or strong relationships with the body fat percentages derived via DXA [30]. However, the strength of the relationships differed among equations used, with an equation developed in 1966 by John Faulkner [32] having the strongest relationship with DXA [29].
The results from these studies demonstrate the lack of agreement between equations, and inconsistent outcomes when compared with more precise body composition assessment methods, such as DXA.

Suarez-Arrones et al. (2018). Body fat assessment in elite soccer players: cross-validation of different field methods. Science and Medicine in Football, pp.1-6.
As demonstrated by Zemski et al. (2018), all skinfold methods will likely differ from one another and criterion reference methods [33], which prevents their use interchangeably, but when a standardized approach is taken with a chosen skinfold assessment method, the longitudinal changes in body composition will become evident [34].
In other words, it’s arguably more important to pick an equation, or at the very least, a number of skinfold sites to measure, and stick with it, as opposed to jumping from equation to equation or switching assessment methodology.
A Few Sources of Error to Consider
Regardless of the equation used, it’s important to note that the outcomes of estimated body fat percentages stemming from skinfold measurements can vary, tremendously. Substantial intra- and inter-observer variability exists [35, 36]. In addition, differences in equipment used, pinch location, lack of technique standardization, and high inter-subject variability can compromise the equation’s reliability, and validity [1, 7, 33-42]. For example, varying the skinfold site by as little as 1 centimeter can produce significantly different results when experienced practitioners measure the same participant [7, 40].
Summary
The research regarding which skinfold equation(s) most accurately predict body fat percentage in athletes is inconsistent, at best. Factors including age, sport, race, gender, and others, appear to impact equation validity. However, skinfold assessment can also be quite reliable and should be considered as a convenient, practical indicator of intra-individual regional and total body composition change over time. Regardless of the specific skinfold equation used, I advise identifying a pragmatic, population-specific skinfold equation, and sticking with the sites/equation used to assess longitudinal changes in athlete body composition. Although 3-site and 7-site skinfold equations are similar in accuracy, I lean towards collecting data on more sites. In the case that a novel, highly accurate equation is developed, the practitioner will be better suited to apply the novel, more accurate equation with his or her data set. Here are a few major advantages and disadvantages of skinfolds testing:
| Advantages | Disadvantages |
|---|---|
| High reliability if the tester is experienced and consistent | Low validity, and very low validity in larger subjects |
| Low cost | Tester expertise required |
| Quick to execute | High inter-tester variability (i.e. reliability can be poor when the tester does not remain the same) |
| Minimal equipment and subject participation required | Most skinfold calipers have an upper limit of 45–60 mm, limiting their use to moderately overweight subjects |
| No technology necessary | Prediction equations may only be valid in the population in which they are derived |
| Allows for regional body fatness assessment | Some subjects may feel uncomfortable stripping down to bare skin in front of the tester |
References
- Fosbøl, M.Ø. and Zerahn, B., 2015. Contemporary methods of body composition measurement. Clinical Physiology and Functional Imaging, 35(2), pp.81-97.
- Wagner, D.R. and Heyward, V.H., 1999. Techniques of body composition assessment: a review of laboratory and field methods. Research Quarterly for Exercise and Sport, 70(2), pp.135-149.
- Meyer, N.L., Sundgot-Borgen, J., Lohman, T.G., Ackland, T.R., Stewart, A.D., Maughan, R.J., Smith, S. and Müller, W., 2013. Body composition for health and performance: a survey of body composition assessment practice carried out by the Ad Hoc Research Working Group on Body Composition, Health and Performance under the auspices of the IOC Medical Commission. British Journal of Sports Medicine, pp.bjsports-2013.
- Harrison, G.G., Buskirk, E.R., Carter, J.L., Johnston, F.E., Lohman, T.G., Pollock, M.L., Roche, A.F. and Wilmore, J.A.C.K., 1988. Skinfold thicknesses and measurement technique. Anthropometric Standardization Reference Manual, 1988, pp.55-80.
- Heyward, V.H., 1996. Evaluation of body composition. Sports Medicine, 22(3), pp.146-156.
- Olds, T., Stewart, A., Carter, L. and Marfell-Jones, M., 2006. International standards for anthropometric assessment. Potchefstroom (ZA): International Society for Advancement of Kinanthropometry.
- Ackland, T.R., Lohman, T.G., Sundgot-Borgen, J., Maughan, R.J., Meyer, N.L., Stewart, A.D. and Müller, W., 2012. Current status of body composition assessment in sport. Sports Medicine, 42(3), pp.227-249.
- Wang, J., Thornton, J.C., Kolesnik, S. and Pierson, R.N., 2000. Anthropometry in body composition: an overview. Annals of the New York Academy of Sciences, 904(1), pp.317-326.
- Edwards, D.A.W., 1950. Observations on the distribution of subcutaneous fat. Clinical Science, 9, pp.259-270.
- Keys, A. and Brozek, J., 1953. Body fat in adult man. Physiological Reviews, 33(3), pp.245-325.
- Jackson, A.S. and Pollock, M.L., 1978. Generalized equations for predicting body density of men. British Journal of Nutrition, 40(3), pp.497-504.
- Jackson, A.S., Pollock, M.L. and Ward, A.N.N., 1980. Generalized equations for predicting body density of women. Medicine and Science in Sports and Exercise, 12(3), pp.175-181.
- Durnin, J.V. and Womersley, J.V.G.A., 1974. Body fat assessed from total body density and its estimation from skinfold thickness: measurements on 481 men and women aged from 16 to 72 years. British Journal of Nutrition, 32(1), pp.77-97.
- Biaggi, R.R., Vollman, M.W., Nies, M.A., Brener, C.E., Flakoll, P.J., Levenhagen, D.K., Sun, M., Karabulut, Z. and Chen, K.Y., 1999. Comparison of air-displacement plethysmography with hydrostatic weighing and bioelectrical impedance analysis for the assessment of body composition in healthy adults–. The American Journal of Clinical Nutrition, 69(5), pp.898-903.
- Gately, P.J., Radley, D., Cooke, C.B., Carroll, S., Oldroyd, B., Truscott, J.G., Coward, W.A. and Wright, A., 2003. Comparison of body composition methods in overweight and obese children. Journal of Applied Physiology, 95(5), pp.2039-2046.
- Ginde, S.R., Geliebter, A., Rubiano, F., Silva, A.M., Wang, J., Heshka, S. and Heymsfield, S.B., 2005. Air displacement plethysmography: validation in overweight and obese subjects. Obesity Research, 13(7), pp.1232-1237.
- Peterson, M.J., Czerwinski, S.A. and Siervogel, R.M., 2003. Development and validation of skinfold-thickness prediction equations with a 4-compartment model. The American Journal of Clinical Nutrition, 77(5), pp.1186-1191.
- Evans, E.M., Rowe, D.A., Misic, M.M., Prior, B.M. and Arngrímsson, S.A., 2005. Skinfold prediction equation for athletes developed using a four-component model. Medicine and Science in Sports and Exercise, 37(11), pp.2006-2011.
- López-Taylor, J.R., González-Mendoza, R.G., Gaytán-González, A., Jiménez-Alvarado, J.A., Villegas-Balcázar, M., Jáuregui-Ulloa, E.E. and Torres-Naranjo, F., 2018. Accuracy of Anthropometric Equations for Estimating Body Fat in Professional Male Soccer Players Compared with DXA. Journal of Sports Medicine, 2018.
- Silva, A.M., Fields, D.A., Quitério, A.L. and Sardinha, L.B., 2009. Are skinfold-based models accurate and suitable for assessing changes in body composition in highly trained athletes?. The Journal of Strength & Conditioning Research, 23(6), pp.1688-1696.
- Shakibaee, A., Faghihzadeh, S., Alishiri, G.H., Ebrahimpour, Z., Faradjzadeh, S., Sobhani, V. and Asgari, A., 2015. How accurate are the anthropometry equations in in Iranian military men in predicting body composition?. Asian Journal of Sports Medicine, 6(4).
- O’Neill, D.C., Cronin, O., O’Neill, S.B., Woods, T., Keohane, D.M., Molloy, M.G. and Falvey, E.C., 2016. Application of a sub-set of skinfold sites for ultrasound measurement of subcutaneous adiposity and percentage body fat estimation in athletes. International Journal of Sports Medicine, 37(05), pp.359-363.
- O’Neill, D.C., Cronin, O., O’Neill, S.B., Woods, T., Keohane, D.M., Molloy, M.G. and Falvey, E.C., 2016. Application of a Sub-set of Skinfold Sites for Ultrasound Measurement of Subcutaneous Adiposity and Percentage Body Fat Estimation in Athletes. International Journal of Sports Medicine, 37(05), pp.359-363.
- Müller, W., Horn, M., Fürhapter-Rieger, A., Kainz, P., Kröpfl, J.M., Maughan, R.J. and Ahammer, H., 2013. Body composition in sport: a comparison of a novel ultrasound imaging technique to measure subcutaneous fat tissue compared with skinfold measurement. British Journal of Sports Medicine, 47(16), pp.1028-1035.
- Wagner, D.R., Thompson, B.J., Anderson, D.A. and Schwartz, S., 2018. A-mode and B-mode ultrasound measurement of fat thickness: a cadaver validation study. European Journal of Clinical Nutrition, p.1.
- Civar, S., Ozer, K., Aktop, A., Tercan, E. and Ayceman, N., 2003. Validity of leg-to-leg bioelectrical impedance measurement in highly active males. Biology of Sport, 20(3), pp.209-220.
- Wilmore, J.H. and Behnke, A.R., 1969. An anthropometric estimation of body density and lean body weight in young men. Journal of Applied Physiology, 27(1), pp.25-31.
- Reilly, T., George, K., Marfell-Jones, M., Scott, M., Sutton, L. and Wallace, J.A., 2009. How well do skinfold equations predict percent body fat in elite soccer players?. International Journal of Sports Medicine, 30(08), pp.607-613.
- Withers, R.T., Craig, N.P., Bourdon, P.C. and Norton, K.I., 1987. Relative body fat and anthropometric prediction of body density of male athletes. European Journal of Applied Physiology and Occupational Physiology, 56(2), pp.191-200.
- Suarez-Arrones, L., Petri, C., Maldonado, R.A., Torreno, N., Munguía-Izquierdo, D., Di Salvo, V. and Méndez-Villanueva, A., 2018. Body fat assessment in elite soccer players: cross-validation of different field methods. Science and Medicine in Football, pp.1-6.
- Deurenberg, P., Weststrate, J.A. and Seidell, J.C., 1991. Body mass index as a measure of body fatness: age-and sex-specific prediction formulas. British Journal of Nutrition, 65(2), pp.105-114.
- Faulkner, J.A., 1966. Physiology of swimming. Research Quarterly. American Association for Health, Physical Education and Recreation, 37(1), pp.41-54.
- Zemski, A.J., Keating, S.E., Broad, E.M., Marsh, D.J., Hind, K. and Slater, G.J., 2018. Pre-season body composition adaptations in elite Caucasian and Polynesian rugby union athletes. International Journal of Sport Nutrition and Exercise Metabolism, pp.1-24.
- Zemski, A.J., Keating, S.E., Broad, E.M. and Slater, G.J., 2018. Longitudinal changes in body composition assessed using DXA and surface anthropometry show good agreement in elite rugby union athletes. International Journal of Sport Nutrition and Exercise Metabolism, 20(XX), pp.1-8.
- Aandstad, A., Holtberget, K., Hageberg, R., Holme, I. and Anderssen, S.A., 2014. Validity and reliability of bioelectrical impedance analysis and skinfold thickness in predicting body fat in military personnel. Military Medicine, 179(2), pp.208-217.
- Nagy, E., Vicente-Rodriguez, G., Manios, Y., Béghin, L., Iliescu, C., Censi, L., Dietrich, S., Ortega, F.B., De Vriendt, T., Plada, M. and Moreno, L.A., 2008. Harmonization process and reliability assessment of anthropometric measurements in a multicenter study in adolescents. International Journal of Obesity, 32(S5), p.S58.
- Lozano-Berges, G., Gómez-Bruton, A., Matute-Llorente, Á., Julián-Almárcegui, C., Gómez-Cabello, A., González-Agüero, A., Casajús, J.A. and Vicente-Rodríguez, G., 2017. Assessing fat mass of adolescent swimmers using anthropometric equations: a DXA validation study. Research Quarterly for Exercise and Sport, 88(2), pp.230-236.
- Fonseca-Junior, S.J., Oliveira, A.J., Loureiro, L.L. and Pierucci, A.P.T., 2017. Validity of skinfold equations, against dual-energy x-ray absorptiometry, in predicting body composition in adolescent pentathletes. Pediatric Exercise Science, 29(2), pp.285-293.
- Santos, D.A., Dawson, J.A., Matias, C.N., Rocha, P.M., Minderico, C.S., Allison, D.B., Sardinha, L.B. and Silva, A.M., 2014. Reference values for body composition and anthropometric measurements in athletes. PloS One, 9(5), p.e97846.
- Hume, P. and Marfell-Jones, M., 2008. The importance of accurate site location for skinfold measurement. Journal of Sports Sciences, 26(12), pp.1333-1340.
- Ducker, K., Kerr, D. and Hume, P., 2018. Best Practice Protocols for Physique Assessment in Sport. In Best Practice Protocols for Physique Assessment in Sport.
- Larson-Meyer, D.E., Woolf, K. and Burke, L., 2018. Assessment of nutrient status in athletes and the need for supplementation. International Journal of Sport Nutrition and Exercise Metabolism, 28(2), pp.139-158.